ASSIGNMENT 4

BY

SHADRECK S CHITSONGA

THE MEDIANS OF A TRIANGLE

In this write up I will explore some of the interesting properties of the medians of a triangle. Let us first of all define a median.

A median of a triangle is a line segment that joins the vertex of a triangle to the midpoint of the opposite side.

There are some basic facts about the medians, which I will just mention and can be explored easily in GSP. Here are some of them:

a. In any triangle there can only be three medians.

b. In an equilateral triangle all the medians are of the same length.

c. In an isosceles triangle, the two medians drawn from

the vertices of the equal angles are equal in length.

d. In a scalene all the medians are of different length.

e. The medians are always inside the triangle.

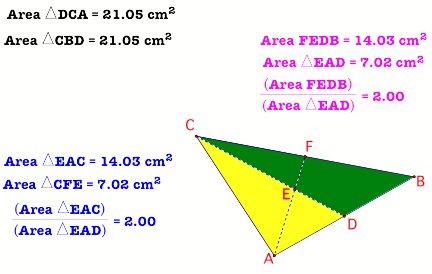
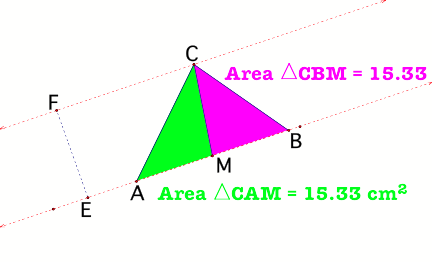
1. MEDIANS AND AREA

One median

Figure 1

From the diagram in figure 1 we see that the two triangles CMA and BCM are equal in area. We can come up with a conjecture and say that, the median of a triangle divides the triangle into two triangles with equal areas.

To show that this is always true we can write a short proof:

Area of any triangle = half the base x height.

In the triangles CMA and CBM, AM and MB are the bases respectively. The two triangles have the same height.

Therefore area of triangle CMA= ½(AM)(FE)

And area of triangle CBM=1/2(MB) (FE)

From the two areas we see that FE=FE (the two triangles have the same height).

Also AM=MB (M is the midpoint of AB, since AM is the median of the triangle. This then means that the two triangles are equal in area.

Now let us consider two medians. Look at the diagram below. We want to see if we can say anything else about the areas.

We have already seen that the median divides the triangle in two equal areas.

Let us extend that and see what happens when we put in the second median.

Look at the GSP diagram in figure 2

Two medians

Figure 2

We have already shown than the median divides the triangle into two triangles of equal areas (look at the green triangle and the yellow triangle).

Let us say that CD is the first median, this divides the triangle as explained above. Now consider the second median, AF. It intersects with the first one at E. We notice that the second median divides the green and yellow triangles in the ratio 1:2. We can write a conjecture here,

If a median one median of a triangle is drawn, the second median to be drawn will divide the areas of the two triangles formed by the first median in the ratio 1:2.

We will postpone the proof for now as we proceed to the case where there are three medians.

Three medians

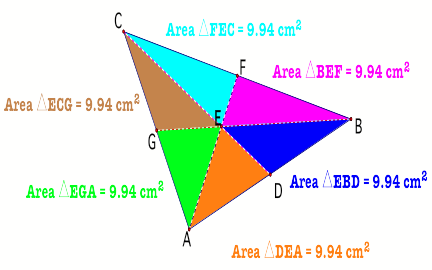
Figure 3

From the areas calculated it is easy to see that after drawing all the three medians the original triangle is divided into six triangles that are all of the same area. Another thing we have noticed is that the three medians are meeting at the same point (All they are concurrent).

Conjecture

Three medians of a triangle divide the triangle into six triangles that are all equal in area.

PROOF

Let us use the same triangle ABC we have in figure 3.

Triangles AED and EDB have the same attitude since they share the same vertex and are sitting on the same base AB.

But we know that D is the midpoint of AB (CD is the median).

It then follows that the area of triangle AED is equal to the area of triangle EDB.

Earlier on when we considered the case of two medians we saw that the second median divided the two triangles formed by the first median in the ratio 2:1. Using that argument we know that the area of triangle AED is 1/3 the area of triangle CAD.

Similarly the triangles GAE and CGE are also equal in area. This means that the area of triangle GAE =area of triangle CGE =1/3 area of triangle CAD.

We can now conclude that the triangles GAE, CGE, CAD and EAD are all equal in area. The rest of the proof is trivial.

CONCURRENCY

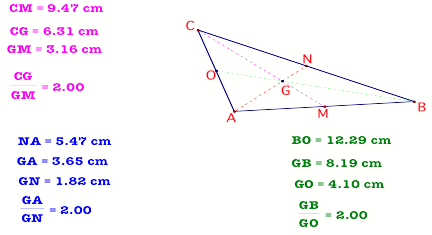
Figure 4

From figure 4 we see two important things

1. The medians are concurrent.

2. The medians of a triangle intersect each other in the ratio 2:1

Proof

There are a number of theorems that we need to look at before we doing the proof. Here I will simply state the theorems (formal proofs are omitted, but are part of secondary school mathematics)

1. Mid-Segment theorem

A line joining the midpoints of two sides of a triangle is parallel to the

third side and equal to half of it.

2. If a pair of opposite sides are equal and parallel, the quadrilateral is a

parallelogram.

3. Diagonals of a parallelogram bisect each other.

We start the proof as follows.

Construction: Let the three medians meet in G. Let Q be the midpoint of GB, P the midpoint of AG, K the midpoint of CG

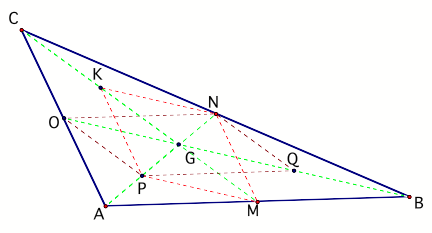
PROOF: PQ is parallel to AB and also PQ=1/2 AB (mid segment theorem)

ON is parallel to AB and also ON=1/2 AB (mid segment theorem)

This means that PQ=ON and PQ is parallel to ON.

We can conclude here that the quad OPQN is a parallelogram

(Theorem). Also we know that diagonals of a parallelogram bisect

each other. In this case PN intersects with OQ in G. We can also

argue that the median AN intersects with the median BO at G.

Using the same argument that we used to show that OPQN is a parallelogram, we can show that KPMN is also a parallelogram.

Similarly the diagonals of KPMN intersect and bisect each other at the point G, also the median CM intersects with the median BO in G.

From above we know that the median BO intersects with the median AN in G, therefore G must be the common point where all the three medians are meeting. So the three medians are concurrent.

For us to show that the medians intersect each other in the ratio 2:1, we can just use the results from above. We have already proved that OPQM and KPMN are parallelograms.

We know also that diagonals of a parallelogram bisect each other.

This means then that in parallelogram OPQN, OG =GQ. But we also know through construction that GQ =QB. Therefore OG=GQ=QB=1/3 OB. ( or BG=2/3OB)

Using the same argument we can say that AP=PG=GN = 1/3 AN(or AG=2/3AN).

In the same manner we can show that CG=2/3 CM.

The conclusion is therefore that the medians of a triangle intersect each other in the ratio 2:1

Remember earlier on we had a conjecture that when one median of a triangle is drawn the second median divides the triangle formed by the first median in the ratio 1:2. Now we are ready to write the proof:

We now know that the medians of triangle intersect each other in the ratio 2:1. Let us consider the triangle CDA. Our results show that its area is 3times the area of triangle GAD. These triangles are sitting on the same base CD and share the same vertex “A”, so they have the same altitude.

Area of triangle CAG = 1/2 CG times the altitude

Area of triangle GAD = 1/2 GD times the altitude

= CG

GD

= 2/3 CD

1/3 CD

=2

1

NOTE: There are still a number of things that can be explored

about the medians of a triangle. Here I concentrated on the

areas and concurrency.